- Research article
- Open access
- Published:
Reversible uptake of molecular oxygen by heteroligand Co(II)–l-α-amino acid–imidazole systems: equilibrium models at full mass balance
Chemistry Central Journal volume 11, Article number: 90 (2017)
Abstract
Background
The paper examines Co(II)–amino acid–imidazole systems (where amino acid = l-α-amino acid: alanine, asparagine, histidine) which, when in aqueous solutions, activate and reversibly take up dioxygen, while maintaining the structural scheme of the heme group (imidazole as axial ligand and O2 uptake at the sixth, trans position) thus imitating natural respiratory pigments such as myoglobin and hemoglobin. The oxygenated reaction shows higher reversibility than for Co(II)–amac systems with analogous amino acids without imidazole. Unlike previous investigations of the heteroligand Co(II)–amino acid–imidazole systems, the present study accurately calculates all equilibrium forms present in solution and determines the \(K_{{{\text{O}}_{2} }}\)equilibrium constants without using any simplified approximations. The equilibrium concentrations of Co(II), amino acid, imidazole and the formed complex species were calculated using constant data obtained for analogous systems under oxygen-free conditions. Pehametric and volumetric (oxygenation) studies allowed the stoichiometry of O2 uptake reaction and coordination mode of the central ion in the forming oxygen adduct to be determined. The values of dioxygen uptake equilibrium constants \(K_{{{\text{O}}_{2} }}\) were evaluated by applying the full mass balance equations.
Results
Investigations of oxygenation of the Co(II)–amino acid–imidazole systems indicated that dioxygen uptake proceeds along with a rise in pH to 9–10. The percentage of reversibility noted after acidification of the solution to the initial pH ranged within ca 30–60% for alanine, 40–70% for asparagine and 50–90% for histidine, with a rising tendency along with the increasing share of amino acid in the Co(II): amino acid: imidazole ratio. Calculations of the share of the free Co(II) ion as well as of the particular complex species existing in solution beside the oxygen adduct (regarding dioxygen bound both reversibly and irreversibly) indicated quite significant values for the systems with alanine and asparagine—in those cases the of oxygenation reaction is right shifted to a relatively lower extent. The experimental results indicate that the “active” complex, able to take up dioxygen, is a heteroligand CoL2L′complex, where L = amac (an amino acid with a non-protonated amine group) while L′ = Himid, with the N1 nitrogen protonated within the entire pH range under study. Moreover, the corresponding log \(K_{{{\text{O}}_{2} }}\) value at various initial total Co(II), amino acid and imidazole concentrations was found to be constant within the limits of error, which confirms those results. The highest log \(K_{{{\text{O}}_{2} }}\) value, 14.9, occurs for the histidine system; in comparison, asparagine is 7.8 and alanine is 9.7. This high value is most likely due to the participation of the additional effective N3 donor of the imidazole side group of histidine.
Conclusions
The Co(II)–amac–Himid systems formed by using a [Co(imid)2]n polymer as starting material demonstrate that the reversible uptake of molecular oxygen occurs by forming dimeric μ-peroxy adducts. The essential impact on the electron structure of the dioxygen bridge, and therefore, on the reversibility of O2 uptake, is due to the imidazole group at axial position (trans towards O2). However, the results of reversibility measurements of O2 uptake, unequivocally indicate a much higher effectiveness of dioxygenation than in systems in which the oxygen adducts are formed in equilibrium mixtures during titration of solutions containing Co(II) ions, the amino acid and imidazole, separately.
Background
The capability of compounds called natural respiratory pigments to reversibly absorb molecular oxygen has been the subject of intensive research since the end of the 19th Century and has been inspiring the creation of artificial systems to imitate their activity [1,2,3,4,5,6,7,8,9,10,11,12,13,14]. Example models of synthetic oxygen carriers include mixed complexes of the type Co(II)–auxiliary ligand–imidazole, in which imidazole coordinates in trans position against the bound O2 molecule, alike imidazole of the proximal histidine in myoglobin and hemoglobin [15]. In contrast to classical methods of preparing such compounds by mixing separate solutions of Co(II) salts, appropriate amino acids and imidazole [16,17,18], an original method has been applied, in which cobalt(II) and imidazole were introduced in the form of a polymeric, pseudo-tetrahedral, semi-conductive complex [Co(imid)2]n. This results in the formation of definite, unique structures with an imidazole molecule in an axial position opposite the O2 molecule [19,20,21,22,23,24,25,26].
[Co(imid)2]n is a coordination compound crystallizing in an infinite polymeric net, in which each cobalt(II) ion is joined via imidazole bridges with four adjacent ions of the metal [27, 28]. Each Co(II) ion forms two dative bonds with the nitrogen atoms of two deprotonated imidazole moieties and two ionic bonds with the nitrogen atoms of two other imidazoles (Fig. 1). Therefore, this alternative method of obtaining dioxygen complexes with a strictly defined structure by starting from the [Co(imid)2]n polymer is much more effective than the method in which appropriate so-called “active” complexes capable of reversible dioxygen uptake are formed in an equilibrium mixture during titration of a solution containing Co(II) ions, the suitable auxiliary ligand (e.g. amino acid) and imidazole [16, 17].
The peculiar property of O2 transport in such Co(II)–amac–Himid systems, as with the natural dioxygen carriers, results from the rapidly stabilizing equilibrium present in solution between the “active” form and the dioxygen-containing form. The “active” form, responsible for the dioxygen transport, is usually a paramagnetic, high-spin, hexacoordinate Co(II) complex of CoII(amac)2(Himid)(H2O) composition, containing two chelate–like connected amino acid molecules forming an equatorial plane, as well as two axial ligands–imidazole and water. After substitution of the dioxygen molecule for water, a dimeric, diamagnetic [CoIII(amac)2(Himid)]2O2 2− complex is formed with the O2 molecule coordinated in peroxide order i.e. with a O2 2− (μ-peroxy) bridge between two cobalt ions formally oxygenated to Co(III). This complex, because of the eventual partial irreversible oxidation of Co(II) to mononuclear Co(III) products, is frequently denoted as an intermediate oxygen adduct. Owing to the elongation of the dioxygen bond from 120.7 pm for the triplet O2 to 149.0 pm for the peroxide O2 2− anion, the oxygen adducts may be used as intermediate complexes in catalytic processes [29,30,31,32,33,34].
The O2 2− bridge (μ-peroxy) exists within pH = 3–9, but upon a rise in basicity above pH 10, this is transformed into a poorly reversible dibridged Co(III)O2 2−OH−Co(III) (μ-peroxy–μ-hydroxy) form. This double-bridge appears in place of the two carboxyl groups, which easily undergo dissociation and which are found in cis position towards the coordinated dioxygen molecule. Such a complex is a much less effective O2 carrier due to its higher affinity for autoxidation. An alternative known description of the oxygen bridges is the form type η, corresponding to “side on” bridge μ-peroxy structures [35]. In turn, acidification of the solution at a low temperature (−3 to 0 °C) leads to protonation of the μ-peroxy bridge, whereas the forming intermediate Co(III)O2 2−H+Co(III) product undergoes a rapid decay accompanied by Co(III) ion formation. In addition, at a temperature around 0 °C and in acidic medium, the O2 2− (μ-peroxy) bridge may be subsequently oxidized by means of strong oxidizers, e.g. Ce4+, MnO4 − or Cl2 ions. As a result, a paramagnetic, stable {[CoIII(amac)2(Himid)]2O2 −}+ complex is formed, with an irreversibly bound dioxygen moiety in the Co(III)–O2 −–Co(III) (μ-superoxy) bridge.
All known O2 carriers (both natural and synthetic) form complexes of two types: monomeric, with an M:O2 stoichiometry of 1:1, and dimeric, with an M:O2 stoichiometry of 2:1. An analysis of the theoretically estimated values of the free standard Gibbs energy of the O2 reactions with metal ions and their complexes could be expected to favor the dimeric structures. In fact, the ΔG° value for the dimer formation reaction attains negative values for a much higher number of metals than is the case for monomer formation. This effect refers to the displacement of complex-formation decidedly to the right [36]. The data find a practical confirmation because among all the known dioxygen carriers, in aqueous solution we observe formation of stable dimeric complexes.
Previous investigations of the Co(II)–amac–Himid systems have not included the key aspect, i.e. accurate calculations of the Co(II), amac and Himid concentrations at equilibrium, by using the formation constants reported in our work for analogous oxygen-free systems [37]. These calculations may allow the equilibrium concentrations of all equilibrium forms present in solution to be determined, and for the \(K_{{{\text{O}}_{2} }}\) equilibrium constants to be evaluated without using any simplified approximations, which for instance take into account only the “active” complex and the oxygen adduct within the mass balance system [19, 38]. Moreover, the advantage of the experimental methods used in the present work, i.e. a direct gas–volumetric experiment with simultaneous pH measurement, is that it allows the degree of reversibility of O2 uptake to be taken into account. As for many other complexes, including a majority of complexes with amino acids and peptides, the irreversible part of the reaction is quite rapid (e.g. t1/2 <5 min for glygly), which excludes the use of the most commonly applied method based only on potentiometric titration [39,40,41].
Results and discussion
The optimum amac to Co(II) ratio equaled 2:1. Above this value, the amount of dioxygen taken up did not change (see Additional file 1: Figure S1). The amount of imidazole released from the [Co(imid)2]n moiety as a result of the mixed Co(II)–amac–Himid–O2 complex formation (0.3 mol Himid per 0.3 mol Co) indicates that the stoichiometric Co(II): imidazole ratio was 1:1, which confirms that one of the two [Co(imid)2]n imidazole moieties remains in the coordination sphere of cobalt(II) of the final complex (see Additional file 2: Figure S2). In other words the structure of the forming dioxygen adducts are unified by the presence of one imidazole in the coordination sphere.
Investigations of oxygenation of the Co(II)–amac–Himid systems indicated that dioxygen uptake is accompanied by a rise in pH to 9–10. An example of the time dependence between pH and the number of mmoles of bound dioxygen is shown for l-α-histidine in Fig. 2. The percentage of reversibility noted after acidification of the solution to the initial pH ranged within ca 30–60% for l–α–alanine, 40–70% for l-α-asparagine and 50–90% for l-α-histidine; this rose as the share of the amino acid in the Co(II): amac: Himid ratio increased (Table 1). The results confirm that the axial imidazole plays a role in enhancing reversibility of the O2 uptake as opposed to the systems with the same amino acids but lacking imidazole [42]. Imidazole is in fact an important complement of the coordination sphere of the central ion as a donor of a free-electron pair of the N3 nitrogen.
In comparison with the system with histidine, the systems with alanine and asparagine demonstrated some higher values for the share of the free Co(II) ion and the particular complex species existing in solution apart from the oxygen adduct (regarded as the entire amount of cobalt engaged in both reversible and irreversible oxygenation) Fig. 3. For the two amino acids, the oxygenation reaction is right shifted to a relatively lower extent. The competitive binary complexes CoL3 (or CoL2 for histidine), which are able to reversibly take up dioxygen, are also present in solution in relatively low concentrations below 0.2% (Fig. 3); according to Fallab’s rule, they have a sufficient number of 3N in the coordination sphere [40]. However, the experimental results indicate that the only active complexes taking up dioxygen in practice are heteroligand species with imidazole as the second ligand (Additional file 2: Figure S2). Therefore, the \(K_{{{\text{O}}_{2} }}\) equilibrium constants can be calculated using formula (16), where the “active” complex is an appropriate heteroligand species with a concentration directly following the full mass balance equation. The fact that the value of log \(K_{{{\text{O}}_{2} }}\) remained constant between different initial total Co(II), amino acid and imidazole concentrations, within limits of error (Table 2), indicates that the “active” complex was a heteroligand CoL2L′complex for alanine and asparagine (Fig. 4), but also for histidine although the structure differs in participation of the N3 nitrogens of the additional imidazole side group (Fig. 5). The imidazole N1–H side-group does not dissociate in the measurable pH range due to it having a pK of 14.4 [43]. In addition, for histidine, as in the case of alanine and asparagine, the dioxygen substitutes a relatively weak donor, i.e. the deprotonated carboxyl oxygen, instead of the water molecule.
Percentage share of free Co(II) ion and complex forms at fixed equilibrium of O2 uptake reaction in the Co(II)–amac–Himid–O2 systems. l-α-amino acid (amac) = a alanine, b asparagine, c histidine. Internal diagrams show the equilibrium share of species other than the O2 adduct in an extended scale. Cadd O2 denotes the total concentration of the dioxygen adduct(with dioxygen bound both reversibly and irreversibly). L amac, L′ Himid. Molar ratio Co(II): amac: Himid = 0.3: 0.6:0.3 (mmol)
The optical absorption spectra for the Co(II)–amac–Himid system with histidine indicate a significant increase of the molar absorption coefficients resulting from the O2 uptake (Fig. 6); similar observations have been reported for analogous systems with alanine and asparagine [38]. The low energetic asymmetric d–d band in curve (a) can be attributed to the asymmetric, quasi-octahedral T 1g→T 1g(P) transition of the Co(H2O) 2+6 aquo-ion. Curve (b) is a spectral curve mainly characterizing the formed heteroligand CoL2L′ active complex, predominating at pH ~9 under oxygen-free conditions, with a blue-shifted d–d band at λ max 485 nm (ε max ~20). Curve (c) corresponds to a μ-peroxo-type dioxygen adduct with two components of the LMCT band from the split antibonding π*(O2) orbital of dioxygen to the unfilled dσ*(Co) orbital: π*h → dσ* (in-plane) and π*v→dσ* (out-of-plane). It can be seen that the molar absorption coefficient of both the bands (ε max ~5 × 104) is much higher than that of the “active” complex. The intensity of the two LMCT components was relatively comparable, this being typical of monobridged peroxo complexes, which are usually non-planar [38, 44].
As can be seen in Table 2, the highest value of log \(K_{{{\text{O}}_{2} }}\) occurs for the histidine system, most likely due to participation of the aforementioned additional effective N3 donor of the histidine imidazole side group. This is not surprising as it is already known that for histidine, the “active” complex is the most thermodynamically stable complex also under oxygen-free conditions [37]. On the other hand, the lower value of log \(K_{{{\text{O}}_{2} }}\) for the asparagine system in comparison with the alanine system is most likely due to steric hindrance, which arises from one of the asparagine amide side groups during formation of the dimer. In this case, a greater share of the amino acid in the Co(II): amac: Himid molar ratio favorably displaces the equilibrium towards oxygen adduct formation. This also makes it possible to obtain chemically reasonable (positive) solutions of equation system (1) at higher excesses of the amino acid (cf. Table 2). For the two remaining amino acids alanine and histidine, particularly histidine, the oxygen adduct (for both the reversible and irreversible parts together) almost entirely uses up the accessible cobalt when the share of the amino acid greatly exceeds the stoichiometric ratio Co(II): amac:Himid = 1:2:1; the concentrations of the other complex species, including the “active” complex, fall to such low levels that it is impossible for the equation system (1) to converge in the form of three positive solutions.
Conclusions
At a decreased temperature close to 0 °C, the Co(II)–amac–Himid systems demonstrate enhanced reversible uptake of molecular oxygen. Coordination of the dioxygen molecule by the “active” complex occurs as exchange of the axial H2O or carboxyl oxygen to O2, occurring together with simultaneous formal intramolecular redox oxidation of Co(II) to Co(III) and the reduction of the charge of the dioxygen molecule to a bridging peroxide O2 2− ion.
The log \(K_{{{\text{O}}_{2} }}\) values are highest for the oxygenated forms of the heteroligand complexes with histidine, as their coordination sphere is formed by a chelating tridentate ligand (with imidazole, NH2, COO− donors). The essential impact on the electron structure of the dioxygen bridge, and by that on reversibility of O2 uptake, is due to the first of the groups mentioned above. The two remaining amac ligands engaged in the mixed complexes (i.e. alanine and asparagine) were bidentate ligands. Even the potentially tridentate l-α-asparagine behaves as a bidentate ligand in the attainable pH range of around 9–10, illustrated in Table 1, which follows also from the previous reports concerning oxygen–free conditions. However, the reversibility of O2 uptake in the latter systems containing an axial imidazole, unequivocally indicates a much higher reversibility than that previously reported for Co(II)–amac systems in the absence of imidazole.
Chemically reasonable (positive) values of both [Co(II)], [amac], [Himid] equilibrium concentrations and hence, appropriate log \(K_{{{\text{O}}_{2} }}\) values, could be attained only for limited Co(II):amac:Himid molar ratios, irrespective of the degree of equilibrium displacement towards oxygen adduct formation.
Experimental
Reagents
l-α-amino acids: asparagine, pure, Sigma Chemical Co., histidine, pure (≥99.0%), Fluka Chemie GmbH, alanine, pure, International Enzymes Limited; polymeric [Co(imid)2]n complex prepared by A. Vogt, Faculty of Chemistry, University of Wrocław [27, 38, 45]; potassium nitrate (V), p.a., P.O.Ch. Gliwice; nitric (V) acid, p.a., P.O.Ch. Lublin; sodium hydroxide—0.5021 M solution determined by potassium hydrogen phthalate; acetone, p.a., P.O.Ch. Gliwice; oxygen pure medical (99.7–99.8%); argon, p.a. (99.999%) from Linde Gas (Poland).
Apparatus
An isobaric laboratory set for volumetric and pH-metric measurements (see Additional file 3: Figure S3), composed of the following elements: a double-walled thermostated glass vessel of volume ca 80 mL, tightly closed with a silicon stopper and equipped with a burette nozzle supplying the 4 M HNO3; a combination pH glass electrode C2401, Radiometer (Copenhagen); a Radiometer Analytical 101 temperature sensor; a gas inlet tube (dioxygen) connected with the gas burette; outlet tube; a glass rode to hang a small glass vessel with the [Co(imid)2]n polymer. A PHM 85 Precision pH Meter Radiometer (Copenhagen), a Fisherbrand FBC 620 cryostat, Fisher Scientific, an Electromagnetic Stirrer ES 21H (Piastów, Poland), an oxygen tank with reducing valve and a CO-501 Oxygen Meter, Elmetron (Zabrze, Poland) were also used. The following glass set was used to determine the imidazole released from the coordination sphere of the mixed complexes: suction flask, water suction pump, washer, Schott funnel POR 40 (see Additional file 4: Figure S4).
Measurement procedures
Oxygenation reaction of the Co(II)–l-α-amino acid–imidazole systems
The thermostated vessel was filled with a solution containing an exactly weighted sample of chosen amino acid, so as to obtain a predicted Co(II)–amac–Himid ratio when adding the [Co(imid)2]n polymer. Adjustment of the solution to constant ionic strength I = 0.5 M was achieved by means of potassium nitrate. The solution was topped up with water to 30 mL. A small glass vessel with 0.3 mmol of the [Co(imid)2]n polymer (hence the same 0.6 mmol of imid) was hung from a glass rod over the solution surface. After the entire vessel reached a temperature close to 0 °C [decrease of temperature inhibits the irreversible oxidation of Co(II)], the initial pH and the initial volume level in the gas burette was read and the main experiment started by inserting the polymer into the sample. The current values of pH and dioxygen volume were noted in definite time intervals up to saturation. A rise in pH was observed along with a change in color from entirely colorless to brown or even dark-brown. At the end of oxygenation, which occurred when reaching pH ≈9 to 10, the solution was acidified to the initial pH with a small aliquot of 4 M nitric acid solution. This caused a partial discoloration of the solution and evolution of dioxygen. The volume of dioxygen evolved against the total volume of dioxygen bound served as a measure of reversibility of oxygenation.
Determination of reaction stoichiometry of dioxygen uptake in the Co(II)–l-α-amino acid–imidazole systems by the molar ratio method
For each system under study, a dependence plot of the number of bound O2 (mmol) against the C L/C M ratio was prepared, where C L—total amac concentration, C M—total Co(II) concentration, which enabled the determination of stoichiometry of dioxygen uptake.
Confirmation of the coordination mode of the central ion by determination of the number of imidazole released from the coordination sphere of the Co(II)–l-α-amac–imidazole–O2 system
Exactly weighed samples of amino acid and the [Co(imid)2]n polymer were placed into a washer so as to attain a molar ratio of Co(II):l-α-amac: imidazole = 0.3: 0.9: 0.3 (mmol). The washer immersed in ice was filled with 2 mL of argonated water and then, during 15 min, the forming “active” complex was argonated continuously. After 10 min, argonation was changed to oxygenation. The final content of the washer, the freshly formed dioxygen complex, was quantitatively added to a Schott funnel previously filled with oxygenated acetone. The oxygen complex, insoluble in water, precipitated as a dark brown solid. At the moment a water suction pump was connected to the Schott funnel. Acetone was filtered off together with the water containing the imidazole released along with oxygen complex formation. The filtrate obtained was titrated potentiometrically with nitric acid. All the steps of experiment were carried out at temperature close to 0 °C.
Calculations of equilibrium concentrations of Co(II), amac and Himid as well as evaluation of the equilibrium \(K_{{{\text{O}}_{2} }}\) constants
The calculations were performed by means of a Mathcad 13 computer program [46]. The mass balance non–linear equation system was solved by the Levenberg–Marquardt method [47, 48], which enables a faster convergence of the solutions than the Gauss–Newton iteration. Such effect is due to the introduction of an additional λ parameter to the Gauss–Newton iteration formula, which corrects the appropriate direction of the procedure depending on whether the solutions go close to or far from the convergence series.
The procedure used the corresponding equilibrium concentrations [M], [L], [L′] (where: [M] = [Co(II)]), which were the searched unknown quantities x 1, x 2, x 3 of the following system:
The solution vector of the system:
follows Newton’s formula:
after an appropriate initial estimation of the X 0 vector. The function vector is:
whereas the matrix of derivatives, i.e. Jacobi matrix, is:
(F’(X))−1 in Eq. (3) denotes the inverted Jacobi matrix.
In the mass balance system all the ligand (both amac and Himid) protonation constants as well as the complex–formation constants with Co(II) were known from the previous reports [37, 45]. In cumulative form the formation constants may be written as:
The functions used for the equation systems of l-α-alanine and l-α-asparagine were due to the fact that the mixed ML2L′ complex capable of dioxygen uptake (existing outside of the non-active mixed MLL′ complex) contains the sufficient three nitrogen donors in the coordination sphere, in accordance with Fallab’s “3 N” rule [49]:
For l-α-histidine, the mixed not oxygen binding complex was a MLL′H species, in which the side group imidazole was protonated at the N3 nitrogen, thus the number of nitrogen atoms in the coordination sphere of the central ion was two, i.e. less than the minimum suggested by Fallab’s rule. However, as the number of nitrogen atoms was sufficient in the “active” complex ML2L′, capable of O2 was as follows:
where: C M—total concentration of the metal: Co(II), C L—total concentration of the l-α-amino acid, \(C_{{L^{\prime}}}\)—total concentration of imidazole, \(C_{{{\text{O}}_{2} }}\)—concentration of the oxygen adduct, β ml —summary stability constants of the Co(II)–l-α-amino acid complexes, β ml’ —summary stability constants of the Co(II)–imidazole complexes, β mll’ —summary stability constants of the mixed Co(II)– l-α-alanine/asparagine–imidazole complexes, β 1210, β 1111—summary stability constants of the mixed Co(II)–l-α-histidine–imidazole complexes.
The hydrolyzed Co(II) aqua-ion and the protonated (not complexed) ligand forms were considered in expressions:
where: K OH—hydrolysis constant of tshe Co(II) aqua-ion = 10−9.8 [50], β LH, β LH2, β LH3—summary (overall) protonation constants of the l-α-amino acid, β L’H—protonation constant of imidazole.
It is noteworthy that solving the nonlinear equation system at very erroneous initial estimations may lead to quite different results or lack of convergence. However, in the case of the systems under study, the solutions [M], [L] and [L′] are not allowed to be negative numbers and they should be found within the limits of zero and the total concentrations C M, C L, C L′. This makes it possible to reject the solutions without a chemical meaning.
The used summary protonation constants of l-α-amino acids and imidazole, the stability constants of the primary Co(II)–amac, Co(II)–Himid complexes, as well as the stability constants of the heteroligand Co(II)–l-α-amino acid–imidazole complexes have been determined previously in the same medium and the same ionic strength as in the present work (KNO3, I = 0.5) [37, 45]. The only different parameter was the temperature: 25.0 °C, instead of 0–1 °C. The lack of data due to the lower temperature is usually caused by lowered sensibility of the glass electrodes. Nevertheless, the systematic error of the stability constants recently used could be estimated on the basis of corresponding literature data as 0.1–0.2 in logarithm [51].
The obtained equilibrium concentrations [M], [L], [L′] were needed to calculate the \(K_{{{\text{O}}_{2} }}\) constant. In the present reaction scheme, the first step corresponded to formation of the “active” complexes:
Consecutively the “active” complex takes up dioxygen by forming the dimeric oxygen adduct:
By treating the O2 uptake as a reversible reaction:

the equilibrium constant may be calculated from the formula:
where [O2 adduct]—equilibrium concentration of this part of the oxygen adduct, in which dioxygen was bound reversibly. The value was found by using the percentage of reversibility of O2 uptake, that is to say by rejecting the part of O2 adduct, in which the metal undergoes irreversible oxidation to Co(III) during the experiment. The equilibrium [O2] concentration was calculated on the basis of table data of dioxygen solubility in water [52].
According to Henry’s law, if the experiment proceeds at the same temperature but at decreased pressure, the volume of gas dissolved in water (or in a diluted solution) is proportionally lower. Under the experimental conditions we have:
where: V g = 0,04758 mL—table value of dioxygen solubility in 1 L of water, at temperature 1 °C under normal pressure 1013 × 105 Pa. \(p_{{{\text{O}}_{ 2} }}\)—partial pressure of dioxygen in the gas burette.
The \(V_{{{\text{O}}_{ 2} }}\) value gives the [O2] concentration after adjustment to the number of mmoles of O2 dissolved in 1 L of the solution.
Abbreviations
- imid:
-
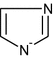
- Himid:
-

- amac:
-
amino acid (α-amine group non-protonated, carboxyl group deprotonated)
- Hamac:
-
amino acid (α-amine group protonated, carboxyl group deprotonated)
References
Tiné MR (2012) Cobalt complexes in aqueous solutions as dioxygen carriers. Coord Chem Rev 256:316–327
Zhang X, Yue F, Li H, Huang Y, Zhang Y, Wen H, Wang J (2016) Reversible oxygenation of -amino acid–cobalt(II) complexes. Bioinorg Chem Appl 2016:3585781
Cheng X, Huang Y, Li H, Yue F, Wen H, Wang J (2016) Reversible oxygenation of 2,4-diaminobutanoic acid-Co(II) complexes. Bioinorg Chem Appl 2016:8296365
Yue F, Song N, Huang Y, Wang J, Xie Z, Lei H, Zhang X, Fu P, Tao R, Chen X, Shi M (2013) Reversible oxygenation of bis[β-(2-pyridyl)-α-alaninato]Co(II) complex in aqueous solution at room temperature. Inorg Chim Acta 398:141–146
Loew G (2006) Electronic structure of heme sites. In: Solomon EI, Lever ABP (eds) Inorganic electronic structure and spectroscopy, 2nd edn. Wiley Interscience, New York, pp 451–532
Wirstam M, Lippard SJ, Friesner RA (2003) Reversible dioxygen binding to hemerythrin. J Am Chem Soc 13:3980–3987
Momenteau M, Reed CA (1994) Synthetic heme dioxygen complexes. Chem Rev 94:659–698
Stenkamp RE (1994) Dioxygen and hemerythrin. Chem Rev 94:715–726
Magnus KA, Ton-That H, Carpenter JE (1994) Recent structural work on the oxygen transport protein hemocyanin. Chem Rev 94:727–735
Niederhoffer EC, Timmons JH, Martell AE (1984) Thermodynamics of oxygen binding in natural and synthetic dioxygen complexes. Chem Rev 84:137–203
Jones RJ, Summerville DA, Basolo F (1979) Synthetic oxygen carriers related to biological systems. Chem Rev 79:139–179
Klotz IM, Kurtz DM Jr (1984) Binuclear oxygen carriers: hemerythrin. Acc Chem Res 17:16–22
Erskine RW, Field BO (1976) Reversible oxygenation in structure and bonding. Springer-Verlag 28:1–50
Henrici-Olivé G, Olivé S (1974) Die Aktivierung von molekularem Sauerstoff. Angew Chem 86:1–56
Collman JP, Fu L (1999) Synthetic models for hemoglobin and myoglobin. Acc Chem Res 32:455–463
Khatoon Z, Kabir-ud-Din (1989) Potentiometric studies on mixed-ligand complexes of cobalt(II) and nickel(II) with amino acids as primary ligands and imidazole as secondary ligand. Trans Met Chem 14:34–38
Brodsky NR, Nguyen NM, Rowan NS, Storm CB, Butcher RJ, Sinn E (1984) pKa and isomer determinations of cobalt(III) imidazole and histidine complexes by NMR and X-ray crystallography. Inorg Chem 23:891–897
Mishra RK, Thakur BG (2016) Studies on some novel mixed ligand complexes of cobalt(II)-imidazol-amino acids. AIJRFRANS 16–146:39–41
Jeżowska-Trzebiatowska B, Vogt A, Kozłowski H, Jezierski A (1972) New Co(II) complexes, reversibly binding oxygen in aqueous solution. Bull Acad Pol Sci 3:187–192
Jeżowska-Trzebiatowska B (1974) Complex compounds as models of biologically active systems. Pure & Appl Chem 367-390
Vogt A, Kufelnicki A, Jeżowska-Trzebiatowska B (1990) Studies on the cobalt(II)–dipeptide–imidazole system; a new dioxygen carrier. Polyhedron 9:2567–2574
Vogt A, Kufelnicki A, Leśniewska B (1994) The distinctive properties of dioxygen complexes formed in the cobalt(II)–asparagine–OH− systems (in relation to other amino acids and mixed complexes with N-base). Polyhedron 13:1027–1033
Kufelnicki A, Świątek M, Vogt A (1995) Uptake of molecular oxygen by Co(II) chelates with peptides in an aqueous solution. Part IX. Ternary cobalt(II)–istidine containing dipeptide-imidazole systems— effective dioxygen carrires. Polish J Chem 69:206–212
Kufelnicki A, Świątek M (1999) Uptake of molecular oxygen by Co(II) chelates with peptides in an aqueous solution. Part XI. Stereoselective properties of oxygenated diastereoisomeric dipeptide systems. Polish J Chem 73:579–592
Kufelnicki A, Pająk M (2003) Dioxygen uptake by ternary complexes cobalt(II)–amino acid–imidazole. Ann Pol Chem Soc 2:467–471
Kufelnicki A, Pająk M (2007) Mass balance in the equilibrium system Co(II)–imidazole–O2. Ann Pol Chem Soc 410–413
Świątek-Tran B, Kołodziej HA, Tran VH, Baenitz M, Vogt A (2003) Magnetism of Co(C3H4N2)2(CO3)(H2O)2. Phys Stat Sol(a) 196:232–235
Baraniak E, Frejman HC, James JM, CE Nockolds (1970) Structural and spectroscopic study of carbonatodiaquobisimidazolecobalt(II), a bidentate carbonato-complex of cobalt(II). J Chem Soc 2558–2566
Das D, Lee YM, Ohkubo K, Nam W, Karlin KD, Fukuzumi S (2013) Temperature-independent catalytic two-electron reduction of dioxygen by ferrocenes with a copper(II) tris[2-(2-pyridyl)ethyl]amine catalyst in the presence of perchloric acid. J Am Chem Soc 135:2825–2834
Fukuzumi S, Tashini L, Lee YM, Ohkubo K, Nam W, Karlin KD (2012) Factors that control catalytic two- vs four-electron reduction of dioxygen by copper complexes. J Am Chem Soc 134:7025–7035
Goifman A, Gun J, Gelman F, Ekeltchik I, Lev O, Donner J, Bornick H, Worch E (2006) Catalytic oxidation of hydrogen sulfide by dioxygen on CoN4 type catalyst. Appl Catal B Environ 63:296–304
Hassanein M, Gerges S, Abdo M, El-Khalafy S (2005) Catalytic activity and stability of anionic and cationic water soluble cobalt(II) tetraarylporphyrin complexes in the oxidation of 2-mercaptoethanol by molecular oxygen. J Mol Catal A Chem 240:22–26
Khandar AA, Nejati K, Rezvani Z (2005) Syntheses, characterization and study of the use of cobalt(II) schiff-base complexes as catalysts for the oxidation of styrene by molecular oxygen. Molecules 10:302–311
Simándi LI, Simándi TM, May Z, Besenyei G (2003) Catalytic activation of dioxygen by oximatocobalt(II) and oximatoiron(II) complexes for catecholase-mimetic oxidations of o-substituted phenols. Coord Chem Rev 245:85–93
Mäcke HR, Williams AF (1988) Dioxygen-transition metal complexes in Fox MA, Chanon M Photoinduced electron transfer. Part D. Photoinduced electron transfer reactions: inorganic substrates and applications. Elsevier Science Publishers BV, New York
Ochiai EI (1973) Oxygenation of cobalt(II) complexes. J Inorg Nucl Chem 35:3375–3389
Woźniczka M, Vogt A, Kufelnicki A (2016) Equilibria in cobalt(II)–amino acid–imidazole system under oxygen-free conditions: effect of side groups on mixed-ligand systems with selected l-α-amino acids. Chem Centr J 10:14
Vogt A (1980) Ph.D. Thesis. Institute of Chemistry University of Wrocław
Stadherr LG, Martin RB (1973) Stereoselectivity in dipeptide complexes of Cobalt(III). Inorg Chem 12:1810–1814
McLendon G, Martell AE (1976) Inorganic oxygen carriers as models for biological systems. Coord Chem Rev 19:1–39
Yatsimirskii KB, Nemoskalenko VV, Aleshin VG, Bratushko YuI, Moiseenko EP (1977) X-ray photoelectron spectra of mixed oxygenated cobalt(II)–amino acid–imidazole complexes. Chem Phys Lett 52:481–484
Bagger S, Gibson K (1972) Reaction of molecular oxygen with mixed cobalt(II) complexes containing (S)–alanine and heterocyclic nitrogen bases. Acta Chem Scand 26:2972–2974
Kiss T (1990) Complexes of amino acids. In: Burger K (ed) Biocoordination chemistry: coordination equilibria in biologically active systems. Ellis Horwood Ltd, Chichester, pp 56–134
Lever ABP (1984) Inorganic electronic spectroscopy, 2nd edn. Elsevier, Amsterdam, pp 285–296
Woźniczka M, Pająk M, Vogt A, Kufelnicki A (2006) Equilibria in cobalt(II)–amino acid–imidazole system under oxygen-free conditions. Part I. Studies on mixed ligand systems with l-α-alanine. Polish J Chem 80:1959–1966
Mathcad 13 (2005) User’s Guide. Mathsoft Engineering & Education, Inc Cambridge
Meloun M, Havel J, Högfeldt E (1988) Computation of solution equilibria. Ellis Horwood Ltd, Chichester
Leggett DJ (1985) The determination of formation constants: an overview of computational methods for data processing. In: Leggett DJ (ed) Computational methods for the determination of formation constants. Plenum Press, New York
Fallab S (1967) Reactions with molecular oxygen. Angew Chem 79:500–511
Baes CF Jr, Mesmer RE (1976) The hydrolysis of cations, New York
Kiss T (1997) The temperature dependence of stability constants in Pettit L, Powell K Stability constants database SC-database for Windows, Appendix 11. IUPAC, Academic Software
Küster FW, von Thiel bearbeitet A, Ruland A (1985) Rechentafeln für die Chemische Analytik. Walter de Gruyter, Berlin
Authors’ contributions
All authors contributed equally in the development of the manuscript. MP carried out the potentiometric and volumetric measurements as well as calculations, participated in the Results and Discussion. MW participated in the UV/Vis studies and in the Results and Discussion. AV provided the polymeric complex and participated in the Discussion. AK suggested the research idea, participated in the “Results and discussion” and coordinated the final formulation. All authors read and approved the final manuscript.
Acknowledgements
Financial support of this work by the Medical University of Łódź (Statute Fund No. 503/3-014-02/503-31-001—A. Kufelnicki) is gratefully acknowledged.
Competing interests
The authors declare that they have no competing interests.
Publisher’s Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Author information
Authors and Affiliations
Corresponding author
Additional files
13065_2017_319_MOESM1_ESM.tif
Additional file 1: Figure S1. Determination of stoichiometry of the O2 uptake by the molar ratio method in the Co(II) – amac – Himid – O2 systems. L-α-amino acid (amac) = (a) alanine, (b) asparagine, (c) histidine. C L – total concentration of amac, C Co – total concentration of Co(II). Mmole O2 – number of mmol of dioxygen taken up. All the samples contained 0.3 mmol of Co(imid)2 in 30 mL of solution.
13065_2017_319_MOESM2_ESM.tif
Additional file 2: Figure S2. Titration curve of the water-acetone filtrate obtained when the dioxygen adduct formed in aqueous solution precipitated in acetone. Co(II) : amac : Himid at a molar ratio of 0.3 : 0.9 : 0.3 (mmol); L-α-amino acid (amac) = (a) alanine, (b) asparagine, (c) histidine.
13065_2017_319_MOESM4_ESM.tif
Additional file 4: Figure S4. Laboratory set for determination of imidazole released from the coordination sphereof Co(II): (a) initial preparation, (b) collection of the filtrate.
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The Creative Commons Public Domain Dedication waiver (http://creativecommons.org/publicdomain/zero/1.0/) applies to the data made available in this article, unless otherwise stated.
About this article
Cite this article
Pająk, M., Woźniczka, M., Vogt, A. et al. Reversible uptake of molecular oxygen by heteroligand Co(II)–l-α-amino acid–imidazole systems: equilibrium models at full mass balance. Chemistry Central Journal 11, 90 (2017). https://doi.org/10.1186/s13065-017-0319-8
Received:
Accepted:
Published:
DOI: https://doi.org/10.1186/s13065-017-0319-8







